Googol, matematikteki büyük sayılardan biridir ve 10100‘e eşittir. Başka bir deyişle 1 googol, 1 rakamına yüz sıfır ekleyerek yazılır. Bu terim Amerikalı matematikçi Edward Kasner’ın yeğeni Milton Sirotta (1929–1980) tarafından 1938 yılında kullanılmaya başlanmıştır. Milton bu sırada dokuz yaşındaydı. Kasner bu kavramı Matematik ve Hayal Gücü adlı kitabında da ele almıştır.

Googol büyüklük derecesi bakımından 70 faktöriyele eşdeğerdir (70! yaklaşık olarak 1.198 googola eşittir) ve yalnızca iki asal çarpana sahiptir (her birinden 100’er tane olmak üzere 2 ve 5 çarpanları). İkilik tabanlı sayı sisteminde 1 googol 333 basamaktan oluşur.

Googolun matematiğe çok yararlı olduğu söylenemez. Bu sayı daha çok görünür evrendeki atomik parçacıkların sayılarının karşılaştırılmasında ve olası satrançoyunlarının sayısının hesaplanmasında kullanılır. Edward Kasner bu sayının düşlenemeyecek büyüklükteki bir sayı ile sonsuz çokluğun arasındaki farkı yansıttığını düşünmektedir. Sayının matematikteki kullanımı bununla sınırlıdır.

Googolun geleneksel yazımı şu şekildedir:

1 googol  =  10100
= 10.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000

Bir googol, gözlenebilir evrendeki toplam atom sayısından (1079 ile 1081 arasında olduğu tahmin edilmektedir) büyüktür. Büyük Patlamadan bu yana geçen Planck zamanı bir googoldan azdır (Güncel rakam 8×1060 Planck zamanıdır). Bundan çıkarılabilecek sonuç şudur: Büyük Patlamadan bu yana geçen süre içinde evrendeki tüm parçacıkların olası konumlarının toplam sayısı bir googolu aşabilir ancak bu sayı bir googolplexten çok küçüktür.

Bir küçük googol 2100 (yaklaşık 1.268×1030) ya da 1,267,650,600,228,229,401,496,703,205,376’ya, bir küçük googolplex 22100 ya da yaklaşık 103.8 × 1029‘a eşittir.

Avogadro sayısı, 6.02214179×1023, 12 gram (0.012 kg) karbon atomunun kararlı halindeki toplam 12C izotopu sayısına eşittir. Bu sayı kimya ve fizikte en çok karşılaşılan büyüklüktür. Avogadro sayısı bir googolun dördüncü dereceden kökünden daha küçüktür.

Kara deliklerin buharlaşması Hawking yayınımı yapmalarıyla açıklanmaktadır. Durum böyleyse çok büyük bir kara deliğin buharlaşması için geçmesi gereken süre yaklaşıkbir googol yıldır.

Yetmiş faktöriyel (70!) 1.19785717 × 10100‘e eşittir. Bunun anlamı yetmiş maddenin (ya da insanın) bir dizi boyunca bir googoldan fazla şekilde sıralanabilecek olduğudur.

Shannon sayısı, 10120, olası satranç oyunlarının toplam sayısıdır ve bu sayı bir googoldan büyüktür.

Googolun Arşimet’in Kum Tanecikleri öyküsünde sözü edilen sayıdan (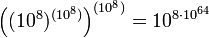\left((10^8)^{(10^8)}\right)^{(10^8)}=10^{8\cdot 10^{64}}) küçük olduğu düşünülmektedir. Ancak, Arşimet‘in kurduğu sistem 108 tabanlı bir sayı sistemiyle benzerlik göstermektedir. Bu nedenle Arşimet’in sayısı şu şekilde yazılabilir:

\left[\left((10)^{(10)}\right)^{10}\right]_{10^8}=\left[10^{100}\right]_{10^8}

Bu, 108 tabanında bir googoldur.

 

Daha fazla bilgi için:

 

http://tr.wikipedia.org/wiki/Googol